git
설명
- Tree 순회
- 다음 네가지 종류가 있다.(traversePreOrder, traverseInOrder, traversePostOrder, traverseLevelOrder)
- BinarySearchTree(이진검색트리)
- 왼쪽 자식이 부모보다 작고, 오른쪽 자식이 부모보다 크다.
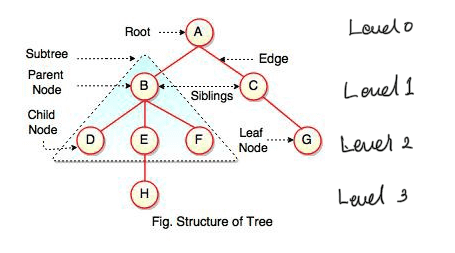
구조
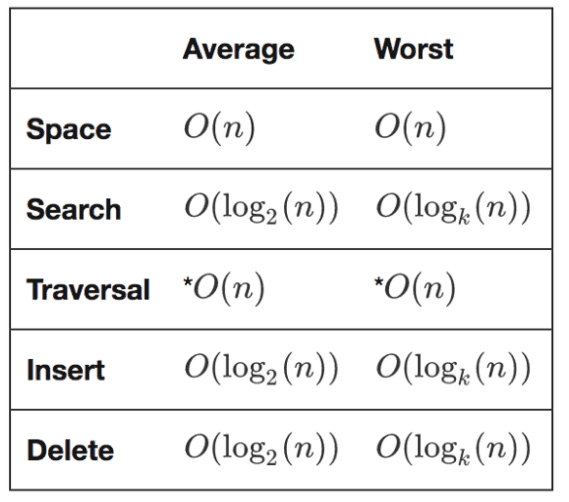
time complexity
구현 List
- node
- Tree 순회
- BinarySearchTree(이진검색트리)
-
연습문제
4.1. 두개 노드의 가장 가까운 공통 node 찾기 * findLowestCommonAncestor(root, value1, value2) 4.2. N level tree 구하기 * printNthLevels(root, n = 0) 4.3. 이진트리가 다른 트리의 하위 트리인지 확인하기 * checkIfSubTree(root, subTree) - isSameTree 호출로 두개 트리가 같은 트리인지 확인 4.4. 인수로 받은 두개 tree가 같은 트리 여부 확인 * isMirrorTrees(tree1, tree2)
node
function TreeNode(value) {
this.value = value;
this.children = [];
}
function BinaryTreeNode(value) {
this.value = value; // root node
this.left = null; // leaf node
this.right = null; // leaf node
}Tree 순회
- 3종류 순회(preOrder, inOrder, postOrder) 각각 recursive, iterator 버전이 있음.
- traverseLevelOrder(단계순위 순회)(== 너비 우선 검색(BFS - breadth first search)
- traversePreOrder
: 재귀 호출 방법으로 아래 traversePreOrderHelper 함수 호출
- traversePreOrderHelper
- traversePreOrderIterative
- traverseInOrder
: 재귀 호출 방법으로 아래 traverseInOrderHelper 함수 호출
- traverseInOrderHelper
- traverseInOrderIterative
- traversePostOrder
: 재귀 호출 방법으로 아래 traversePostOrderHelper 함수 호출
- traversePostOrderHelper
- traversePostOrderIterative
- traverseLevelOrder
: 단계순위 순회(== 너비 우선 검색(BFS - breadth first search) class BinaryTree {
constructor() {
this._root = null;
this.traverseArr = [];
}
// 선순위 순회(재귀호출)
traversePreOrder() {
this.traversePreOrderHelper(this._root);
return this.printTraverse();
}
traversePreOrderHelper(node) {
if (!node) return;
// console.log(node.value);
this.traverseArr.push(node.value);
this.traversePreOrderHelper(node.left);
this.traversePreOrderHelper(node.right);
}
// 선순위 순회(반복문)
/*
# 전략
: nodeStack 배열이 재귀 호출 했을때 stack과 똑같이 동작한다.
step1. 항목을 출력한다.
step2. right leaf node를 nodeStack에 push
step3. left leaf node를 nodeStack에 push
# right leaf node을 먼저 넣는이유는 ?
* let node = nodeStack.pop(); 단계에서 나중에 넣은 왼쪽 자식을 먼저 빼내기 때문이다.
*/
traversePreOrderIterative() {
let nodeStack = [];
nodeStack.push(this._root);
while (nodeStack.length) {
let node = nodeStack.pop();
//step1
// console.log(node.value);
this.traverseArr.push(node.value);
//step2
if (node.right) nodeStack.push(node.right);
//step3
if (node.left) nodeStack.push(node.left);
}
return this.printTraverse();
}
// 중순위 순회(재귀호출)
traverseInOrder() {
//재귀 호출로 트리 순회
this.traverseInOrderHelper(this._root);
return this.printTraverse();
}
traverseInOrderHelper(node) {
if (!node) return;
this.traverseInOrderHelper(node.left);
// console.log(node.value);
this.traverseArr.push(node.value);
this.traverseInOrderHelper(node.right);
}
// 중순위 순회(반복문)
/*
# 전략
step1. currNode가 null이 아닐경우 현재 root node의 left leaf node으로 이동하면서 가장 왼쪽에 있는 노드로 이동
- 이동하면서 root node를 nodeStack 배열에 push
step2.0 currNode = nodeStack 배열에 넣은 node를 pop()
step2.1. step2에서 pop()한 node value 콘솔 찍고
step2.2. currNode = currnode의 right노드
([***] currnode의 right leaf node 여부에 따라 왼쪽 노드를 순회 할지말지 결정된다.)
step2.3. currNode == null && nodeStack이 0일때까지 순회
*/
traverseInOrderIterative() {
let currNode = this._root,
nodeStack = [],
done = false;
while (!done) {
if (currNode != null) {
//step1
nodeStack.push(currNode);
currNode = currNode.left;
} else {
//step2.3
if (nodeStack.length) {
//step2.0
currNode = nodeStack.pop();
//step2.1
// console.log(currNode.value);
this.traverseArr.push(currNode.value);
//step2.2
currNode = currNode.right;
} else {
done = true;
}
}
}
return this.printTraverse();
}
// 후순위 순회(재귀호출)
traversePostOrder() {
this.traversePostOrderHelper(this._root);
return this.printTraverse();
}
traversePostOrderHelper(node) {
if (node.left) {
this.traversePostOrderHelper(node.left);
}
if (node.right) {
this.traversePostOrderHelper(node.right);
}
this.traverseArr.push(node.value);
// console.log(node.value);
}
// 중순위 순회(반복문)
traversePostOrderIterative() {
let stack1 = [],
stack2 = [];
stack1.push(this._root);
while (stack1.length) {
let currNode = stack1.pop();
stack2.unshift(currNode.value);
if (currNode.left) stack1.push(currNode.left);
if (currNode.right) stack1.push(currNode.right);
}
return stack2.join('->');
// while (stack2.length) {
// const node = stack2.pop();
// console.log(node.value);
// }
}
/*
# 단계순위 순회
* == 너비 우선 검색(BFS - breadth first search)
* 핵심
- leaf node(right, left leaf node)로 깊게 들어가며 N level Tree 각 노드 단계를 방문
*/
traverseLevelOrder() {
let root = this._root,
queue = [],
stack = [];
if (!root) return;
queue.push(root);
while (queue.length) {
let currNode = queue.shift();
// console.log(currNode.value);
stack.push(currNode.value);
if (currNode.left) queue.push(currNode.left);
if (currNode.right) queue.push(currNode.right);
}
return stack.join('->');
}
printTraverse() {
const copyTraverseArr = [ ...this.traverseArr ];
this.traverseArr = [];
return copyTraverseArr.join('->');
}
}BinarySearchTree(이진검색트리)
BinarySearchTree 클래스 (extends BinaryTree)
* insert
* remove(deleteRecursively, findMin)
* findNode /*
# 이진 검색 트리
* root보다 작으면 왼쪽, 크면 오른쪽 노드에 위치 한다.
*/
class BinarySearchTree extends BinaryTree {
constructor() {
super();
this._root = null;
}
insert(value) {
let thisNode = {
left: null,
right: null,
value: value
};
if (!this._root) {
this._root = thisNode;
} else {
let currentRoot = this._root;
while (true) {
if (currentRoot.value > value) {
if (currentRoot.left != null) {
currentRoot = currentRoot.left;
} else {
currentRoot.left = thisNode;
break;
}
} else if (currentRoot.value < value) {
if (currentRoot.right != null) {
currentRoot = currentRoot.right;
} else {
currentRoot.right = thisNode;
break;
}
} else {
break;
}
}
}
}
// 시간 복잡도(균형트리) O(log2(n))
// 시간 복잡도(불균형 트리) O(n)
remove(value) {
return deleteRecursively(this._root, value);
//노드보다 작으면 왼쪽 노드로, 크면 오른쪽 노드로 설정하는 이진 검색 트리 특징을 이용
//left node를 찾아가면 가장 작은 숫자의 노드를 찾을 수 있다.
function findMin(root) {
while (root.left) {
root = root.left;
}
return root;
}
function deleteRecursively(root, value) {
if (!root) {
return null;
} else if (value < root.value) {
root.left = deleteRecursively(root.left, value);
} else if (value > root.value) {
root.right = deleteRecursively(root.right, value);
} else {
//value를 찾은 경우
//no child
if (!root.left && !root.right) {
//case1
return null;
} else if (!root.left) {
//case2
root = root.right;
return root;
} else if (!root.right) {
//case2
root = root.left;
return root;
} else {
//case3
// - 자식 노드 두개 있는 경우 왼쪽 하위 트리의 최대치, 또는 오른쪽 하위 트리의 최소치를 찾아서 해당 노드 대체
let tempNode = findMin(root.right);
root.value = tempNode.value;
root.right = deleteRecursively(root.right, tempNode.value);
return root;
}
}
}
}
findNode(value) {
let currentRoot = this._root,
found = false;
while (currentRoot) {
if (currentRoot.value > value) {
currentRoot = currentRoot.left;
} else if (currentRoot.value < value) {
currentRoot = currentRoot.right;
} else {
//노드 찾음
found = true;
break;
}
}
return found;
}
}두개 노드의 가장 가까운 공통 node 찾기
// 연습문제 1. 두개 노드의 가장 가까운 공통 node 찾기
function findLowestCommonAncestor(root, value1, value2) {
function findLowestCommonAncestorHelper(root, value1, value2) {
if (!root) return;
//[point] 조건문
if (Math.max(value1, value2) < root.value) return findLowestCommonAncestorHelper(root.left, value1, value2);
//[point] 조건문
if (Math.min(value1, value2) > root.value) return findLowestCommonAncestorHelper(root.right, value1, value2);
return root.value;
}
return findLowestCommonAncestorHelper(root, value1, value2);
}N level tree 구하기
// ## 연습문제 2. N level 노드 구하기
function printNthLevels(root, n = 0) {
let arrayNth = [];
queue = [];
if (!root) return;
// 너비 우선 검색: 자바스크립트로 하는 자료구조와 알고리즘 p.266 참고(stack별로 stack 구조 그림)
queue.push([ root, 0 ]);
while (queue.length) {
let tuple = queue.shift(),
node = tuple[0],
level = tuple[1];
if (level == n) {
arrayNth.push({ value: node.value, level });
}
if (node.left) queue.push([ node.left, level + 1 ]);
if (node.right) queue.push([ node.right, level + 1 ]);
}
console.log(`${n} 번째 level node list`);
console.log(arrayNth);
}이진트리가 다른 트리의 하위 트리인지 확인하기
/*
# 같은 트리 인지 확인
* checkIfSubTree에서 사용 됨.
* 주어진 두 트리가 구조가 같은지 확인
* return 문 예상 시나리오
- root1, root2의 value가 같으면 해당 노드의 왼쪽을 recursive 하면서 모두 순회하면서 비교
- 그리고 stack에서 빠져나오면 그 다음 조건인 노드의 오른쪽 조건을 확인한다.
*/
function isSameTree(root1, root2) {
if (root1 == null && root2 == null) return true;
if (root1 == null || root2 == null) return false;
return (
root1.value == root2.value &&
isSameTree(root1.left) === isSameTree(root2.left) &&
isSameTree(root1.right) === isSameTree(root2.right)
);
}
// ## 연습문제 3. 이진트리가 다른 트리의 하위 트리인지 확인하기
// : isSameTree를 재귀 호출하면서 subTree가 root의 하위 subTree인지 확인한다.
function checkIfSubTree(root, subTree) {
var queue = [],
counter = 0;
if (!root) {
return;
}
queue.push(root);
while (queue.length) {
let temp = queue.shift();
if ((temp.data == subTree.data) === isSameTree(temp, subTree)) {
return true;
}
if (temp.left) {
queue.push(temp.left);
}
if (temp.right) {
queue.push(temp.right);
}
}
return false;
}인수로 받은 두개 tree가 같은 트리 여부 확인
// # 7. 인수로 받은 두개 tree가 같은 트리 여부 확인
function isMirrorTrees(tree1, tree2) {
if (!tree1 && !tree2) {
return true;
}
if (!tree1 || !tree2) {
return false;
}
const checkLeftwithRight = isMirrorTrees(tree1.left, tree2.right),
checkRightwithLeft = isMirrorTrees(tree2.right, tree1.left);
return tree1.value == tree2.value && checkLeftwithRight && checkRightwithLeft;
}