문제
길이가 n인 철근이 있을 때 이 철근을 팔아서 얻을 수 있는 이익의 최댓값을 구해보자 단, 철근은 길이 1에서 길이 n까지 정수의 길이로 나눠 판매할 수 있으며 길이별 가격표가 주어진다.
해결 방법
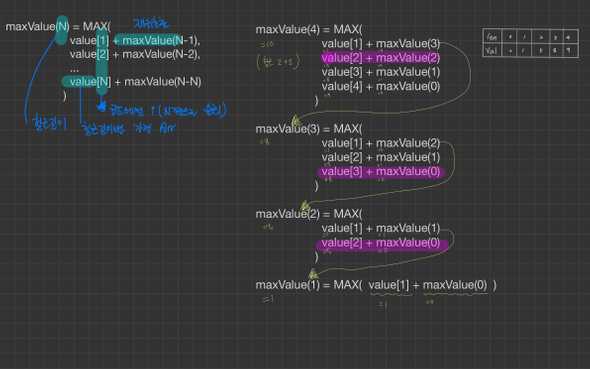
maxValue(N) = MAX(
value[1] + maxValue(N-1),
value[2] + maxValue(N-2),
...
value[N] + maxValue(N-N)
)CODE
const value = [0, 1, 5, 8, 9, 10, 17, 17, 20]
let maxValues = Array(value.length).fill(0)
function MaxValue(barArr, N) {
// 종단점
if (N <= 0) {
return 0
}
// 이미 계산된 값이 있으면 반환
if (maxValues[N - 1] != 0) {
return maxValues[N - 1]
}
// memo 전략
maxValues[N - 1] = Number.MIN_SAFE_INTEGER
//순회/ 재귀호출
for (var i = 1; i <= N; i++) {
//재귀 호출시 N의 범위: N = 0 ~ N-1
//재귀 호출로 철근길이 N을 자를 수 있는 모든 경우의 수를 탐색 할 수 있다.
maxValues[N - 1] = Math.max(
maxValues[N - 1],
value[i] + maxValue(value, N - i)
)
}
return maxValues[N - 1]
}
var barArr = [1, 5, 8, 9, 10, 17, 17, 20]
console.log(MaxValue(barArr, barArr.length))재귀 문제 풀이 로직 예) maxValue(4)
maxValue(4) = MAX(
value[1] + maxValue(3),
value[2] + maxValue(2),
value[3] + maxValue(1),
value[4] + maxValue(0)
)
maxValue(3) = MAX(
value[1] + maxValue(2),
value[2] + maxValue(1),
value[3] + maxValue(0)
)
maxValue(2) = MAX(
value[1] + maxValue(1),
value[2] + maxValue(0)
)
maxValue(1) = MAX( value[1] + maxValue(0) )재귀 문제 풀이 코드 예) maxValue(4)
예) recursive 호출시 maxValue(4) 일때 호출되는 코드
-
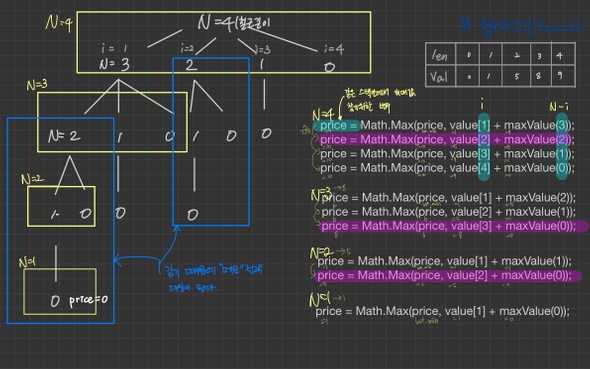
maxValue(4) 일때 for문 순회 안에서 호출되는 코드
price = Math.Max(price, value[1] + maxValue(3)); price = Math.Max(price, value[2] + maxValue(2)); price = Math.Max(price, value[3] + maxValue(1)); price = Math.Max(price, value[4] + maxValue(0)); -
maxValue(3) 일때 for문 순회 안에서 호출되는 코드
price = Math.Max(price, value[1] + maxValue(2)); price = Math.Max(price, value[2] + maxValue(1)); price = Math.Max(price, value[3] + maxValue(0)); -
maxValue(2) 일때 for문 순회 안에서 호출되는 코드
price = Math.Max(price, value[1] + maxValue(1)); price = Math.Max(price, value[2] + maxValue(0)); -
maxValue(1) 일때 for문 순회 안에서 호출되는 코드
price = Math.Max(price, value[1] + maxValue(0));
callstack 순서
- DFS로 탐색한다.
- 대괄호 순서 확인{}
{1}-> maxValue(4) = MAX(
value[1] + maxValue(3) <-{2},
value[2] + maxValue(2) <-{9},
value[3] + maxValue(1) <-{10},
value[4] + maxValue(0) <-{11}
)
{2}-> maxValue(3) = MAX(
value[1] + maxValue(2) <-{3},
value[2] + maxValue(1) <-{7},
value[3] + maxValue(0) <-{8}
)
{3}-> maxValue(2) = MAX(
value[1] + maxValue(1) <-{4},
value[2] + maxValue(0) <-{6}
)
{4}-> maxValue(1) = MAX(
value[1] + maxValue(0) <-{5}
)