문제
n개의 물건이 있으며, 각 물건에는 무게, 가격(weight, value)이 정해져 있다. 이 상점에 도둑이 들어와서 물건을 가져온 배낭 용량 C만큼 물건을 넣을 수 있다. 가져갈 수 있는 물건 가격의 최댓값은?
해결 방법
각 물건을 배낭에 넣을지 말지 두가지 선택이 가능
- 물건을 배낭에 넣을 때
- 이경우 물건은 n-1개 남는다.
- 배낭에 추가로 넣을 수 있는 최대 무게: C-weight[n-1]
- 도둑이 훔친 물건의 가치: value[n-1] 만큼 증가
- n-1개의 물건과 C-weight[n-1]의 무게를 넣을 수 있는 배낭이 있는 원래 문제가 남는다.(재귀호출)
- 물건을 매낭에 넣지 않을때
- 이경우 물건은 n-1개 남는다.
- 배낭에 추가로 넣을 수 있는 최대 무게: C(그대로 유지)
- 도둑이 훔친 물건의 가치: 그대로 유지
- n-1개의 물건과 C의 무게를 넣을 수 있는 배낭이 있는 원래 문제가 남는다.(재귀호출)
CODE
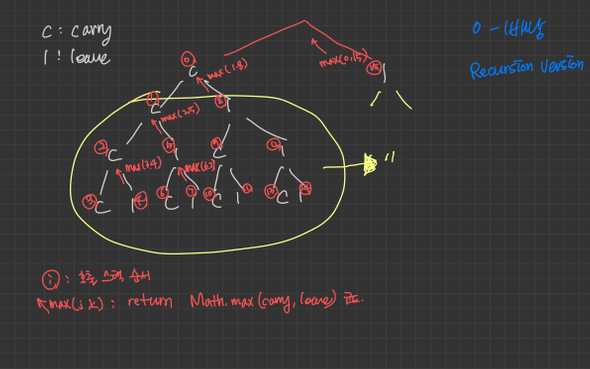
function knapSack(C, weight, value, n) {
// 종단점
if (C <= 0 || n <= 0) return 0
// 물건 무게가 배낭 용량 보다 큰 경우
if (weight[n - 1] > C) {
return knapSack(C, weight, value, n - 1)
}
// n번째 물건을 배낭에 넣는 경우
const carry = value[n - 1] + knapSack(C - weight[n - 1], weight, value, n - 1)
// n번째 물건 인넣는 경우
const leave = knapSack(C, weight, value, n - 1)
return Math.max(carry, leave)
}
const C = 5 // 배낭 용량
const weight = [2, 3, 4, 5] // 물건 무게
const value = [3, 4, 5, 6] // 물건 가격
const n = weight.length // 물건 개수
console.log(knapSack(C, weight, value, n)) // 7 (무게 2 + 3)call stack tree(하향식 접근방법)
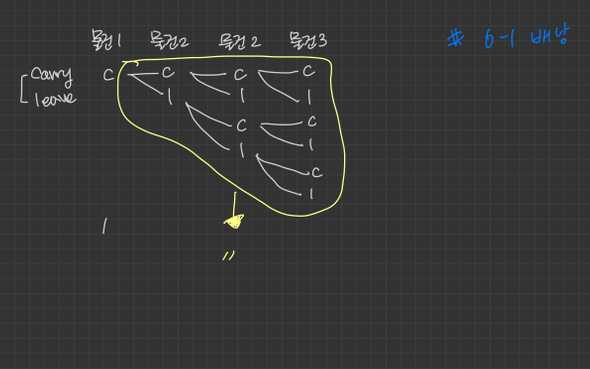
# 물건을 배낭에 넣을 수 있는 모든 경우의 수(전체탐색) 트리 구조
o: 배낭에 물건 넣기
x: 배낭에 물건 안 넣기
o - 물건 무게 2 (첫번째 물건)
o x - 물건 무게 3 (두번째 물건)
o x o x - 물건 무게 4 (세번째 물건)
o x o x o x o x - 물건 무게 5 (네번째 물건)
x - 물건 무게 2 (첫번째 물건)
o x - 물건 무게 3 (두번째 물건)
o x o x - 물건 무게 4 (세번째 물건)
o x o x o x o x - 물건 무게 5 (네번째 물건)ㅎ