n-Queens 설명
- NxN의 체스판에 N개의 퀸을 서로 공격하지 않게 놓는 방법 혹은 그 수를 구하는 문제
- 퀸은 가로, 세로, 대각선 공격할 수 있다.
DFS(깊이우선탐색, Depth First Search),재귀(Recursion),백트래킹(Back tracking),상태공간 트리개념이 필요
DFS
DFS는 트리 구조에서 노드들을 순회하는 방법 중 하나로, 노드가 자식 노드를 가지고 있다면 자식 노드들을 계속해서 파고 들어가는 순회 방식이다.- 자식노드가 아닌 형제 노드를 먼저 순회하는 방식인
BFS(너비우선탐색, Breadth First Search)에 비해 메모리를 적게 차지한다는 장점이 있다. - 원래 DFS는 맨 밑의 자식까지 탐색을 하는 완전탐색 알고리즘이지만, N-Queens에서는
Back-tracking방법과 함께 필요없는 노드는 방문하지 않음으로써 탐색 시간을 줄일 수 있다. - 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 계속 가다가 더 이상 갈 수 없게 되면 다시 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법과 유사하다.
- 즉, 넓게(wide) 탐색하기 전에 깊게(deep) 탐색하는 것이다.
- 사용하는 경우: 모든 노드를 방문 하고자 하는 경우에 이 방법을 선택한다.
- 깊이 우선 탐색(DFS)이 너비 우선 탐색(BFS)보다 좀 더 간단하다.
- 단순 검색 속도 자체는 너비 우선 탐색(BFS)에 비해서 느리다.
- 자기 자신을 호출하는 순환 알고리즘의 형태 를 가지고 있다.
- 전위 순회(Pre-Order Traversals)를 포함한 다른 형태의 트리 순회는 모두 DFS의 한 종류이다.
-
이 알고리즘을 구현할 때 가장 큰 차이점은, 그래프 탐색의 경우 어떤 노드를 방문했었는지 여부를 반드시 검사 해야 한다는 것이다.
- 이를 검사하지 않을 경우 무한루프에 빠질 위험이 있다.
Recursion
- DFS에서 재귀가 사용
- base case로 함수를 종료 시켜 무한루프에 빠지지 않도록 해야한다.
- 답을 못찾으면 for문을 빠져나와 무한루프를 피할 수 있다.
Back tracking
- DFS를 개선한 알고리즘
-
정답이 될 수 없는 노드는 탐색하지 않음으로써 탐색 효율을 높이는 방법
- 가지 않아도 될 길을 배제하여 시간을 단축하는 방법
for (let i = 1; i <= n; i++) {
cols[level + 1] = i // [point] back tracking
if (queens(level + 1)) {
// level+1번째 말을 각각의 열에 놓은 후 recursion을 호출
break
}
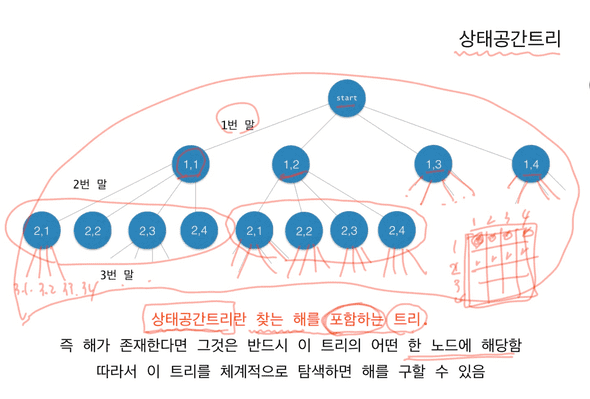
}상태공간트리(state space tree)
설계
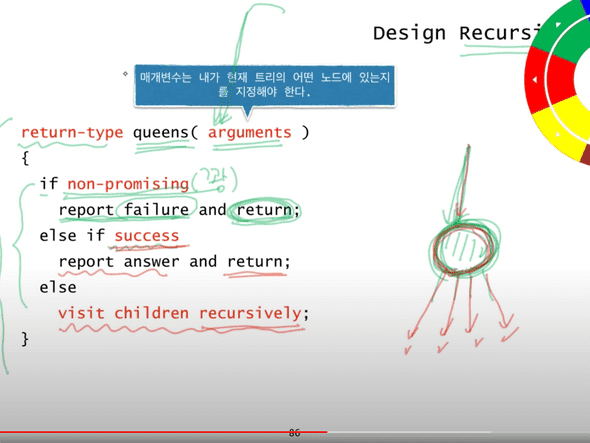
Design Recursion 1
Design Recursion 2
Design Recursion 3
Design Recursion 4
Design Recursion 5.1 - promissing(실현가능한 상태)
Design Recursion 5.2 - promissing(대각선)
-
대간선에 놓여 있는 위치여부 판단 방법
- 가로, 세로 길이가 같으면 대각선에 놓인것
-
row2 - row1 = |col2 - col1|
- row는 row2가 항상 크니까 절대값 필요 x
- col은 col2 > col1 될 수 도 있어 절대값 필요.
- 같으면 대각선상에 놓여 있는 것
-
예) 위치에 놓여져 있는 말 사이의 가로, 세로 길이는?
Design Recursion 5.3 - BackTraking
구현 코드 설명
/*
# POINT: cols 배열의 의미
* row별 말들이 놓이 column
* 예) cols = [2,4,1,3] 의미
- 첫번째 행에는 두번째 열에 퀸
- 두번째 행에는 네번째 열에 퀸
- 세번째 행에는 첫번째 열에 퀸
- 네번째 행에는 세번째 열에 퀸
*/
var cols = [];
var n;
var cnt;
function queens(level) {
// debugger;
if (!promissing(level)) {
return false;
} else if (level === n) {
// # POINT: 종단점 - 체스판 마지막 row에 도착 했을 때
cols.shift();
console.log(cols.toString());
return true;
}
//# visit chidren recursively: promissing을 통과해야 아래 로직을 수행
//# 마지막 퀸 말은 앞에 있는 말들이 놓여있지 않은 곳에 위치하면된다(앞에 있는 말들이 서로 공격안하는 포지션에 위치했으니까)
for (let i = 1; i <= n; i++) {
cols[level + 1] = i;
// level+1번째 말을 각각의 열에 놓은 후 recursion을 호출
if (queens(level + 1)) {
break;
/*
# POINT: return 하지 않는다!
* return 하면 dfs(깊이우선탐색)이 끝나 버린다.
* 그리서, queens에 true나오는 조건(level === n)도달하면 끝내야 한다.
* 즉 한가지 경우의 n-queens밖에 구하지 못한다.
*/
}
}
return false;
}
// 퀸 말들이 row마다 공격 할 수 없는 위치인지 확인
/*
* 행 요소
- 배열 index
* 열 요소
- 배열 값
*/
function promissing(level) {
for (let i = 1; i < level; i++) {
if (cols[i] == cols[level]) {
//같은 열에 놓였는지 검사
return false;
// # abs: 절대값
} else if (level - i == Math.abs(cols[level] - cols[i])) {
// 같은 대각선에 놓였는지 검사
/*
# POINT: 대간선에 놓여 있는 위치여부 판단 방법
- 가로, 세로 길이가 같으면 대각선에 놓인 것
* level - i
- 세로 길이
* cols[level] - cols[i]
- 가로 길이
* row2 - row1 = |col2 - col1|
- row는 row2가 항상 크니까 절대값 필요 x
- col은 col2 > col1 될 수 도 있어 절대값 필요.
- (row2 - row1), (|col2 - col1|)이 같으면 대각선상에 놓여 있는 것
* 예) 위치에 놓여져 있는 말 사이의 가로, 세로 길이는?
- (row, col) => (0,3) (1,2)
- 1-0 = |2-3|
*/
return false;
}
}
return true;
}
function solution(level) {
var answer = 0;
//# level: row index
n = level;
// cols = [...Array(level)]; //queens가 놓이는 위치(array index = row level, 요소 = column )
queens(0);
}
console.log(solution(4));구현 코드
let colsArr = [];
let n1;
let count;
function queens(level) {
// 유효성 검사
if (!promissing(level)) {
return false;
} else if (level === n1) {
colsArr.shift();
console.log(colsArr.toString());
return true;
}
// recursion
for (let i = 1; i <= n1; i++) {
colsArr[level + 1] = i;
if (queens(level + 1)) {
break;
}
}
return false;
}
// 퀸을 놓을 수 있는 여부 확인
function promissing(level) {
// 놓여있는 퀸을 대상으로 모두 비교
for (let i = 1; i < level; i++) {
if (colsArr[i] == colsArr[level]) {
// 같은 열 확인
return false;
} else if (level - i == Math.abs(colsArr[i] - colsArr[level])) {
// 대각선 위치 확인(두 퀸의 가로, 세로 )
return false;
}
}
return true;
}
function solution(level) {
var answer = 0;
n1 = level;
debugger;
queens(0);
}
solution(4);참고
https://gmlwjd9405.github.io/2018/08/14/algorithm-dfs
https://velog.io/@junyong92/Algorithm-N-Queens-vck3jj8f1g